
Electric charges, force and field
In classical mechanics, we find from Newton’s laws, qualitatively as well as quantitatively, how the motion of an object is impacted by what is known as Force.
it is also seen that there are four fundamental forces of nature, electromagnetic force being one of the four.
A simple experiment can demonstrate the existence of electric forces.
When two plastic rods are brought close to each other, there is neither any attraction nor any repulsion between them.

The same thing is observed between two glass rods, or a plastic rod and a glass rod.
If the plastic rods are rubbed with fur, there will be repulsion between them.
Similarly, if the glass rods are rubbed with silk, they will repel each other.
However, a fur-rubbed plastic rod and a silk-rubbed glass rod attract each other.

Scientific investigations have found that these forces, whether attractive or repulsive, are due to electric charges. There are two kinds of electric charge – positive and negative.
The force between two charge particles is called electric force or electrostatic force.
Atomic basis of electrostatics

Matter consists of atoms that are “electrically neutral”. Each atom has a tiny but dense nucleus that comprises positively charged protons and uncharged or neutral neutrons. The number of protons that an atom of a particular element contains is the atomic number Z of that element. Surrounding the nucleus is an equal number (Z) of negatively charged electrons.
Electrically neutral atom: # of electrons = # of protons

When plastic is rubbed with fur, some electrons are transferred from fur to plastic – so the otherwise uncharged plastic becomes negatively charged.

When glass is rubbed with silk, some electrons are transferred from glass to silk – consequently, the uncharged glass becomes positively charged.
In either case, that is, plastic and fur together or glass and silk together, the total number of electrons does not change – electric charge is conserved.
Coulomb's law
The described experiment shows how two charged objects “qualitatively” interact with each other.
Now, we have to look at the “quantitative” nature of this interaction which is derived from experiments by Charles Coulomb.
Force was measured between two objects with respective charges q1 and q2 separated by a distance r.
The size of the objects was much smaller than the distance between them – so that they could be considered as “point charges”

It was found that the magnitude of the force varies inversely as the square of the distance separating the charges and proportional to the product of the charges.

The direction of the force is along the line between the charges.
The force is repulsive if the charges have the same sign while attractive if they have opposite signs.
So, for two point charges, the magnitude of the electric force (also called Coulomb force) is given by

Here charge is measured in Coulomb and force in Newton.
k (electrostatic / Coulomb constant) = 8.9876 x 10 9 N . m 2 / C 2
We can also write ![]()
![]()
is the permittivity constant.
If q1 is at position r1 and q2 at r2, electric force exerted by q1 on q2 is

where r12 = r2 – r1 is the vector pointing from q1 to q2, and
![]()
is a unit vector in the same direction. F12 is radially directed away from q2.
Similarly, the force exerted by q2 on q1 is given by

F21 has the same magnitude as F12 but is opposite in direction.
If q1 and q2 have the same sign – force is repulsive; If they have opposite signs – the force is attractive.
When more than two charges are present, the force between any pair is given by Coulomb’s law.

For three charges q1, q2 and q3, the resultant force exerted by two charges (q1 and q2) on the third (q3) = vector sum of forces the two charges would exert individually, that is,

This is the principle of superposition of electric forces.
If there is a system of n charges q1, q2, …………. , qn,
The net electric force exerted on a specific charge qj by n – 1 other charges is given by the principle of superposition as

.Problem # 1
 Let us consider a charge q1 = 2 mC and a charge q2 = 18 mC held respectively at the origin (x = 0) and x = 1 m.
Let us consider a charge q1 = 2 mC and a charge q2 = 18 mC held respectively at the origin (x = 0) and x = 1 m.
Q1. If a positive charge q3 be placed at x = 0.5 m, which of the following would best describe the motion of q3?
(a) Remain stationary at x = 0.5 m
(b) Move in the + ve direction of x with an acceleration that decreases with time
(c) Move in the – ve direction of x with an acceleration that increases with time
(d) Move in the – ve direction of x with a constant acceleration
(e) Move in the + ve direction of x with a constant acceleration
Q2. What would be the position of q3 so that there is no net force acting on it?
To answer Q1, let us consider the following:
q3 will move if there is a net (nonzero) force acting on it, and
the direction of the net force will be the direction of movement.
Putting in the numerical values we can find that
Magnitude of the force exerted by q1 on q3 is

in the + ve direction of x-axis , and
Magnitude of the force exerted by q2 on q3 is
![]()
in the – ve direction of x-axis
So, the ratio F13 / F23 = 1 / 9
Therefore, Fnet = F13 + F23 is not equal to 0
This rules out (a)
And, since the net force is in the – ve x-direction, (b) and (e) are ruled out
As q3 moves toward q1 and away from q2, F13 increases, F23 decreases and at certain point F13 = F23
So, the net force / acceleration is decreasing (in – ve x-direction) / increasing (in + ve sense) to zero
Ans: (c)
To answer Q2, consider that
When in equilibrium, net force on q3 = 0

q3 is at x, so the distance between q1 and q3 = x , and the distance between q2 and q3 = 1 – x
![]()
On simplification, we have

Positive root of the quadratic equation, x = 0.25 m
Electric field
Coulomb’s law says, F12 = force q1 exerts on q2
But, how does q2 “know” presence of q1?
To answer the question, we have to introduce the concept of Electric Field E.
Particle 1 sets up an “electric field” in surrounding space
When, particle 2 placed in that field it “knows” presence of particle 1
E (vector field): distribution of electric vectors E in space around charged object
Definition: E is the electric force on unit + ve charge (at any point in space)
Mathematically, E = F0 / q0
(E is measured in Newton / Coulomb)
That is,
F0 is the force acting on positive “test charge” q0


So that, F = q E
Visualizing the electric field

As we see, for a charge q located at S (called the source point).
Electric field at P (called the field point)

Magnitude of displacement SP, r = | r |
Unit vector in direction of displacement ![]()
The electric field exists at all points surrounding S, and the magnitude and direction of the field can be determined at any point in that space.

Electric field lines give a visual perspective to electric field.
Electric field vector is tangent to the electric field line / curve at each point.
Field lines for a + point charge are directed radially outward.
(for a – ve point charge they are directed radially inward).

Magnitude of electric field varies along a given field line.
Magnitude proportional to the number of lines through unit surface area.
As seen in the figure, E at P1 > E at P2
Electric field due to two point charges
– generalized case (each charge q)

Charges are located respectively at A and B on the x-axis, at distance d on opposite sides of origin.
Objective: To calculate net electric field at point P on the y-axis.
Magnitude of electric field at point P due to charge at A or B:

Magnitude of x-component

Magnitude of y-component

Specific cases
1. Charges A and B are both positive
Electric field vectors (using unit vectors ![]() )
)

Due to charge at A


Due to charge at B

(- ve sign indicates x-component of in the negative direction of x-axis)
When added, x- components cancel out, and net electric field
![]()
Magnitude: 
is in the positive direction of y-axis

2. A positive, B negative
Magnitude: ![]()
– in the positive direction of x-axis

3. A negative, B negative
Magnitude: ![]()
– in the negative direction of y-axis

4. A negative, B positive
Magnitude: ![]()
– in the negative direction of x-axis
Field lines due to two positive point charges

At any point (say, P1) in the surrounding space, the net electric field E1 is the vectorial addition of the individual fields.
Field E1 at point P1 is tangent to the field line passing through P1 – this line from the charge on the left is not emerging radially outward – but curving upward
Field E2 at point P2 is tangent to the field line passing through P2 – this line from the charge on the right is not emerging radially outward – but curving downward
Overall pattern of the electric
field lines for two positive point
charges
No. of source charges = n
Net force on a test charge q0 at certain point P by the principle of superposition
F0, net = F10 + F20 + . . . . . + Fn0
Electric field at that point

We can write

ri – distance of ith source charge qi from P, and
![]() is the unit vector
is the unit vector
- Electric fields also obey the principle of superposition
A numerical problem:

We have a positive charge q1 at A, and negative charge – q2 at B
| q1| = | q2| = 2 mC d = 1 cm

Objective: To determine the electric field at y = 10 cm
Solution: By symmetry, y-components cancel out
Magnitude of the field is given by

Here, q = 2 x 10 -6 C, d = 10 -2 m, y = 0.1 m
Hence,

– in the positive direction of x-axis

Q2.
As shown in the figure, a square of side d contains a point positive charge +q at the lower right corner, and a point negative charge –q at each of the other three corners. Indicate the direction of the net electric field at point P located at the center of the square.

Ans.
Let us number the corners 1, 2, 3, 4
Taking the charges pairwise,
Field E12 due to the charge pair at 1 and 2 is directed vertically upward
Field E34 due to the charge pair at 3 and 4 is directed horizontally leftward
As E12 = E34
Net field E directed leftward making angle 45° with each of them

Q (in continuation)
What will be the effect of replacement of the point negative charge – q at the upper left corner of the square by a point positive charge + q ?

After the replacement
Field E12 due to the charge pair at 1 and 2 is directed horizontally rightward
Field E34 due to the charge pair at 3 and 4 is directed horizontally leftward
Since E12 and E34 are equal and opposite
Net field E = 0
Electric potential and potential difference
Electric potential is defined in terms of electric potential energy. To understand electric potential energy, let us consider the following:
When a test charge q0 is placed at a point P in an electric field E created by some source charge distribution, it experiences a force q0 E.
As the test charge is moved in the field (casing a displacement), the work done by the field on the charge is equal to the negative of the work done by the external agent.
For a given position of the test charge in the field, the charge-field system has a potential energy U relative to a reference configuration (say, the test charge is at an infinite distance from the source charge distribution) where U = 0.
So, when the test charge moves from the reference configuration to point P, the work done by the electric force on the test charge is denoted by W, where
U = – W
The electric potential at P is then defined as

That is, the electric potential at a point P in an electric field is the amount of electric potential energy when a unit positive charge is brought to the point from infinity.
1 volt = 1 joules per coulomb
If we move a charge from an initial point i to another point f (call it final point for that particular movement) in the electric field, there is a change in the electric potential
![]()
Every charged object or charge distribution sets up electric potential V at points throughout its electric field. If a charge q is placed at a point in the field, the potential energy of the configuration is
U = q V
To be noted that for moving a particle between two points in space, the work done be a conservative force does not depend on the path taken by the particle but only on the initial and final positions.
If a particle with charge q moves from i to f, the potential energy changes by
![]()
Relation between field and potential
A test charge q0 is placed at point P electric field E (created by some source charge distribution) experiences a force, F = q0 E.
For an infinitesimal displacement ds of the point charge q0 in the field, the work done on the charge is

Potential energy of the charge-field system changes by
![]()
For a finite displacement![]() of the charge q0 from point A to point B, the change in the potential energy of the system
of the charge q0 from point A to point B, the change in the potential energy of the system

Then,

is the potential difference between two points A and B.
Definition: The potential difference between two points in an electric field is defined as the change in potential energy of the system when a test charge q0 is moved between the points divided by the test charge.
Let us try to calculate the potential at a distance r (an arbitrary field point P) from a point charge q present at the origin (r = 0).
As we have seen, the field due to the point charge is given by

So, we have the potential difference between the field point and a reference point

where ![]() is the change in r associated with the displacement ds.
is the change in r associated with the displacement ds.
Let us choose the reference point at an infinite distance from the point charge q. Then, replacing VP with V, and setting Vref = 0, we have by integration

Let there be a system of n point charges qi (i = 1, 2, …….. , n). Then, it follows from the principle of superposition of electric fields that the potential due to the system is given by

that is, the sum of the potentials due to each of the charges separately.
In a reverse manner it is possible to calculate the electric field from the electric potential
From
![]()
we can write

If the field has only one component Ex ,

In three-dimension, the electric field components can be evaluated from V (x, y, z)

It should be noted that it is the difference in potential that is meaningful. The electric potential at a field point is based on the assumption that the potential is zero at a convenient reference point.
Further, the potential difference between two field points depends only on a source charge or a source charge distribution. On the other hand, for a potential energy to exist, there must be a system of two or more charges.
Potential energy of a system of two charged particle
If a charge charge q1 sets up an electric field in its surrouding space, work done by an external agent to bring a charge q2 from infinity to a distance r12 from q1 is q2 V1 – this energy is transferred into the system which now has a potential energy

For a system of three charges

Problems on potential and potential energy
#1

A point charge q1 = – 2.0 mC is located at the origin of xy– coordinate system and a point charge q2 = + 4.0 mC is located at (0, 4.0) m. Find the total electric potential at a point P (3.0, 0).

By superposition principle, electric potential at P due to the two charges

Putting in the numerical values

#2
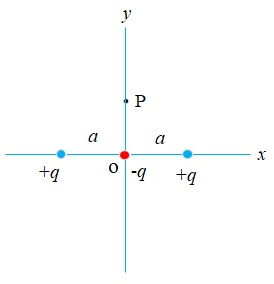
Two positive point charges q each are fixed respectively at x = a and x = – a on the x-axis, while a negative point charge – q is placed at the origin. P is a movable point on the y-axis. Express the electric potential of the system of charges as a function of y and determine the point where the electric potential is zero.
Electric potential due to each + q

and due to – q

Hence, the electric potential due to the system of three charges


That is, 4 y 2 = a 2 + y 2
or, 3 y 2 = a 2
Hence, the electric potential is zero at
![]()
#3
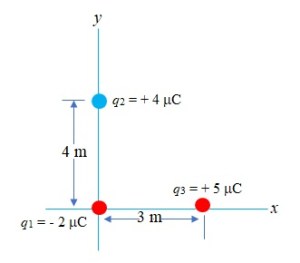
(a) What is the change in potential energy of the two-charge (q1–q2) system is a third point charge q3 = 5 mC is brought to the point point shown in the figure ?
(b) What is the final potential energy of the three-charge system ?
Ans.(a) The change in the potential energy is


Ans.(b) To find total potential energy of the three-charge system, we have to calculate the potential energy of the two-charge system prior to arrival of q3

So, the total potential energy
Utot = U12 + U13 + U23 = – 12 x 10 – 3 J = – 12 mJ